BSidesCbr 2021 ran over the weekend and the cybears put on an excellent CTF. I played with skateboarding dog and we came 1st! It was an overall amazing effort from the whole team. I was able to solve all of the crypto challenges except for Vanity AES and Rot Away Rust. I took a look at Rot Away Rust after the CTF ended and decided to do a writeup for it since it's a great and deceptively easy challenge that didn't get much attention from many teams during the CTF.

The challenge authors have published solution scripts and walkthroughs of their own here. The writeups in this post are to show how I solved the challenges and to give an idea of how I approached them in general. If there's anything I could clarify or explain better feel free to reach out to me on Discord or Twitter!

FunWithPrimes
Despicable Key
ssssh
Empty Vault
Bomb Disposal
Optimal Prime
supergm
Super Cool Facts Server!
Ordinary Course of Business
Rot Away Rust

FunWithPrimes

Primes and number theory are a critical part of cryptography. Try this series of short puzzles to get a flag!

nc funwithprimes.chal.cybears.io 3141

The challenge asks us to solve a series of 5 RSA puzzles:

Given $N = pq, e, p, q$ and a ciphertext, recover the plaintext message.
Given $N = pq$ and $\varphi(N)$ , recover the prime factors of $N$ .
Given $N = pq$ and $p + q$ , recover the prime factors of $N$ .
Given $N = pq$ and $q - p$ , recover the prime factors of $N$ .
Given $N = pq, e, d$ , recover the prime factors of $N$ .

Solution

Stage 1 is just textbook RSA. Compute $\varphi(N) = (p-1)(q-1)$ and $d \equiv e^{-1} \pmod{\varphi(N)}$ , then compute $m \equiv c^d \pmod N$ .

In stages 2, 3 and 4, we are given two equations and we have two unknowns ( $p$ and $q$ ). We can avoid having to do any tedious algebra by simply setting up the equations and using Sage's inbuilt methods. The method of resultants in the solution script below essentially takes two (multivariate) polynomials and returns another polynomial with a variable eliminated. Once we have a polynomial in just one variable, we can easily find its roots with .roots().

Stage 5 is a bit more tricky. We use the fact that $ed \equiv 1 \pmod{\varphi(N)}$ , so $ed = 1 + k \varphi(N)$ . Intuitively, $N \approx \varphi(N)$ and $ed \approx N$ , so in our equation, $k$ is actually quite small. It turns out that $k$ , is small enough to be easily bruteforced. Once we have a candidate for $\varphi(N)$ , we can use the same technique we used for stage 2 to recover the primes.

import json
import os
os.environ['PWNLIB_NOTERM'] = 'True'
from pwn import *
from Crypto.Util.number import *

conn = remote('funwithprimes.chal.cybears.io', 3141)
[conn.recvline() for _ in range(2)]

# Stage 1
data = json.loads(conn.recvline().decode())
N, e, p, q = [data[k] for k in 'Nepq']
c = int(data['cipher'], 16)
d = pow(e, -1, (p-1)*(q-1))
m = pow(int(c), int(d), N)
msg = long_to_bytes(m).split(b'\x00')[1].decode()
conn.sendline(msg)

# for stages 2, 3 and 4
P.<p, q> = PolynomialRing(ZZ)
def solve(f1, f2):
    g = f1.resultant(f2, q)
    roots = g.univariate_polynomial().roots()
    if len(roots) == 0:
        return False
    p_ = abs(roots[0][0])
    q_ = abs(roots[1][0])
    return min(p_, q_)

# Stage 2
conn.recvline()
data = json.loads(conn.recvline().decode())
N, phi = [data[k] for k in ['N', 'phi']]
f1 = (N + 1) - phi - p - q
f2 = N - p*q
conn.sendline(str(solve(f1, f2)))

# Stage 3
conn.recvline()
data = json.loads(conn.recvline().decode())
N, p_plus_q = [data[k] for k in ['N', 'p+q']]
f1 = N - p*q
f2 = p+q - p_plus_q
conn.sendline(str(solve(f1, f2)))

# Stage 4
conn.recvline()
data = json.loads(conn.recvline().decode())
N, q_take_p = [data[k] for k in ['N', 'q-p']]
f1 = N - p*q
f2 = q - p - q_take_p
conn.sendline(str(solve(f1, f2)))

# Stage 5
conn.recvline()
data = json.loads(conn.recvline().decode())
N, e, d = [data[k] for k in 'Ned']
k = 0
while 1:
    k += 1
    phi = int(e*d - 1) // k
    f1 = (N + 1) - phi - p - q
    f2 = N - p*q
    ans = solve(f1, f2)
    if ans:
        conn.sendline(str(ans))
        print(conn.recvline().decode())
        exit()

Flag: cybears{2^82589933-1_15_pr1m3!}

Despicable Key

Help! I've securely encrypted my file. It's OK, I remember the key, but not the IV or the tag... can you help?

## ENCRYPT
## pip install pycryptodomex

from binascii import *
from Cryptodome.Cipher import AES

key = b'cybearscybears20'
import os
n = os.urandom(12)

with open('flag.png', 'rb') as f:
    d = f.read()

a = AES.new(key, AES.MODE_GCM, nonce=n)
cipher, tag = a.encrypt_and_digest(d)

with open('flag.png.enc', 'wb') as g:
    g.write(cipher)

We are given an encrypted PNG file and the script used to encrypt it. The file is encrypted with AES-GCM, and we are given the key.

Solution

To decrypt the file, we need to recover the nonce. When encrypting, the 12 byte IV is padded out to 16 bytes with four extra trailing null bytes. It is then used as a counter as in CTR mode. Looking at the diagram for GCM, we see that the first block of ciphertext is obtained by XORing the first block of plaintext with the encryption of the counter appended to the nonce.

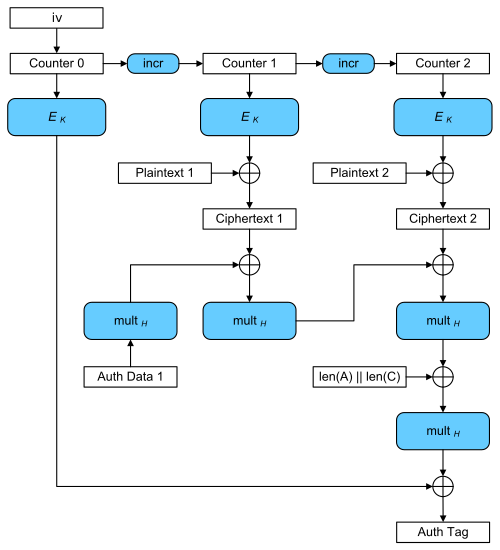
The first 16 bytes of a PNG file are always known, so we can use this information to recover the nonce and counter by XORing the ciphertext with this known plaintext, and then decrypting that result. Once we have the nonce, we can easily decrypt the entire file.

from pwn import xor
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes, bytes_to_long

key = b'cybearscybears20'

enc = open('./flag.png.enc', 'rb').read()
png_hdr = bytes.fromhex('89504E470D0A1A0A0000000D49484452')

ctr_enc = xor(png_hdr, enc[:16])
ctr_p2 = AES.new(key, AES.MODE_ECB).decrypt(ctr_enc)
ctr = long_to_bytes(bytes_to_long(ctr_p2) - 2)
ctr = ctr.rstrip(b'\x00')

data = AES.new(key, AES.MODE_GCM, nonce=ctr).decrypt(enc)
open('flag.png', 'wb').write(data)

Flag: cybears{BeAnOptimistPrimeNotANegatron!}

ssssh

It's a secret! Don't share...

Nothing else is included in the challenge other than the description. The challenge title and description hint towards secret sharing. On the front page of the CTF, there was a commented out URL that lead to a QR code. Decoding the QR code gives the data (3, 0x68d479d61b7f8370d35d1cae227b8d80). We had already figured out that this would be related to some secret sharing problem before the CTF started because of this. We also found a share hidden in the conference badge before the CTF. During the CTF, my teammate found the two remaining shares around the conference hall.

Solution

The idea behind secret sharing is that a secret is split up into shares which are given to the shareholders. The secret is only able to be recovered when a certain number of shareholders combine their shares. This is implemented with polynomials in Shamir's Secret Sharing Scheme:

Suppose a secret $s$ is to be split into $n$ shares, and we want these shares to be such that we need at least $k$ shares to recover the secret. We begin by choosing a random polynomial $f(x)$ of degree $k-1$ such that $f(0) = s$ . Then, $n$ points are distributed to the shareholders. Since $m$ points are required to uniquely define an $m-1$ degree polynomial, it follows that the polynomial $f(x)$ can only be recovered when at least $k$ shares are combined. Once the $k$ shares are combined and $f(x)$ is recovered, the secret is recovered by computing $f(0)$ . The polynomial can be recovered using a technique known as Lagrange interpolation.

On the Wikipedia page, a sample Python implementation is shown with polynomials whose coefficients are in the finite field $\mathbb{F}_p$ for some prime $p$ . However, in the challenge, the finite field $GF(2^{128})$ is used. Sage has a .lagrange_polynomial() method for polynomial rings which makes recovering the secret polynomial from the shares easy.

from Crypto.Util.number import long_to_bytes

F.<y> = GF(2^128)
R.<x> = PolynomialRing(F)

SHARES = [
    (1, 0x7435500906f721eed55d380d8b5ee133),
    (2, 0x982ab13c3a4ee44094007cad86887d8a),
    (3, 0x68d479d61b7f8370d35d1cae227b8d80),
    (4, 0x271458acf640198551280f952e412bc2)
]
SHARES = [map(F.fetch_int, xy) for xy in SHARES]

f = R.lagrange_polynomial(SHARES)
secret = f.constant_coefficient().integer_representation()
print(long_to_bytes(secret).decode())

Flag: cybears{C@r1ng!}

Empty Vault

What is identity? It is the difference between us. Difference is experienced in the mind, yet the Buddha said this mind creates the world, that this world only exists in the mind and nowhere else.

http://mt-vault.chal.cybears.io:31415/

mt_flask.py

We are presented with a simple website where we provide a password as input. The password is hashed with a Merkle tree construction which takes SHA256 hashes of individual bytes/characters as leaves and builds the next level by taking the SHA256 hash of the concatenation of a node's two children. The final hash is the contents of the root node.

Solution

The goal is to submit a password that hashes to the same hash as SuperSecretPassword, without sending SuperSecretPassword itself. Taking a look at the /auth route handler and the validatePassword function, we see that we are actually able to input leaves directly into the Merkle tree as only the transformed parameter is used:

def validatePassword(user_password, password_hashes, denyList=[], debug=False):    
    try:
        joined_password = unhexlify("".join(user_password.split(",")))
    except Exception as e: 
        raise Exception("ERROR: Formatting error. Exiting")
        
    if joined_password in denyList: 
        raise Exception("Nice try, but that password is not allowed...")
    
    # we can directly input leaves by separating them with ","
    split_password = [unhexlify(c) for c in user_password.split(",")]
    user_password_hash = hashPassword(split_password)

    if debug: 
        print("user_password entered: [", user_password, "]")
        print("hashes", password_hashes)
        print("deny list", denyList)
        print("hash", user_password_hash)

    if (user_password_hash in password_hashes): 
        return True

    return False

@app.route('/auth', methods=['GET'])
def do_auth():
    TP = request.args.get('transformed','')
    P = request.args.get('password','').encode()
    
    if P == test_password:
        return 'Nice try, but that password is not allowed :P'

    try:
        res = validatePassword(TP, password_hashes, denyList=[test_password])
    except Exception as e: 
        return str(e)    

    if res:
        return 'Authed! Here is your flag: '+flag
    else:
        return 'Wrong Password'

This diagram from Wikipedia shows how the construction works:

Notice that if we send Hash 0 + Hash 1 as the "transformed" password, then it will be input into the tree as the only leaf. So SHA256(Hash 0 + Hash 1) will be the root. To solve the challenge, we just need to find the contents of the two children nodes of the root in the Merkle tree formed when hashing SuperSecretPassword.

from hashlib import sha256

class MerkleTree(object): 
    def __init__(self):
        self.leaves = list()
        self.levels = None
        self.is_ready = False

    def add_leaf(self, value):         
        self.leaves.append(sha256(value).digest())

    def _calculate_next_level(self):
        solo_leave = None
        N = len(self.levels[0])  # number of leaves on the level
        if N % 2 == 1:  # if odd number of leaves on the level
            solo_leave = self.levels[0][-1]
            N -= 1

        new_level = []
        for l, r in zip(self.levels[0][0:N:2], self.levels[0][1:N:2]):
            new_level.append(sha256(l+r).digest())
        if solo_leave is not None:
            new_level.append(solo_leave)
        self.levels = [new_level, ] + self.levels  # prepend new level

    def make_tree(self):
        self.is_ready = False
        if len(self.leaves) > 0:
            self.levels = [self.leaves, ]
            while len(self.levels[0]) > 1:
                self._calculate_next_level()
        self.is_ready = True

    def get_root_children(self):
        if self.is_ready:
            if self.levels is not None:
                return self.levels[1][0].hex(), self.levels[1][1].hex()
            else:
                return None
        else:
            return None

def get_root_children(p):
    mt = MerkleTree()
    for c in p:
        mt.add_leaf(c)
    mt.make_tree()
    return mt.get_root_children()

test_password = "SuperSecretPassword"
left, right = get_root_children([c.encode() for c in test_password])
print(left + right)

We get the output: 606755aeed86f9892329e3dc622bb285910dea2cab41da929217bb75e569a1ce42343d1bc3021c2e7cd8bcb26928e3dc42be0c3853849888518e888414789a9e. Sending this as the transformed password gives us the flag.

curl http://mt-vault.chal.cybears.io:31415/auth?transformed=606755aeed86f9892329e3dc622bb285910dea2cab41da929217bb75e569a1ce42343d1bc3021c2e7cd8bcb26928e3dc42be0c3853849888518e888414789a9e

Flag: cybears{1_u5e_crypt0_t0_f1ll_th3_3mpt1n355_1ns1d3_my_h34rt!}

Bomb Disposal

There are things to be done. Do them now, or they must be done next time, or the next, or the next.

[You hear a small click] WuKongPrime quietly says "stop walking" while putting a powerful robotic monkey hand on your shoulder. "You've stepped on an abandoned mine. It's now armed. See those numbers being displayed? That's an encrypted count-down. The only way to disarm it is to input the seed value. We have reverse engineered an implementation of the arming sequence, but we haven't cracked it..." [small electronic beeps and the countdown continues] beep ... beep ... beep ...

bomb.py:

from secrets import flag

assert(len(flag) > 512//8)

seed = int.from_bytes(flag, byteorder='big')

class BBSnLCG:
    def __init__(this, seed):        
        this.B = int.from_bytes(b'BSides CBR', byteorder='big')
        this.C = int.from_bytes(b'cybears', byteorder='big')
        this.D = 2020
        this.N = 133329403635104636891429937256104361307834148892567075810781974525019940196738419111061390432404940560467873684206839810286509876858329703550705859195697849826490388233366569881709667248117952214502616623921379296197606033756105490632562475495591221340492570618714533225999432158266347487875153737481576276481
        this.e = 2
        this.rng_state = seed

    def step(this):
        # Linear Congruential Generator part
        # Step the internal state of the RNG
        this.rng_state = (this.B*(this.rng_state**3) + this.C*this.rng_state + this.D) % this.N

    def get_state(this):
        #Blum-Blum-Shub part
        return pow(this.rng_state, this.e, this.N)

if __name__ == "__main__":

    print("Arming bomb...")
    rng = BBSnLCG(seed)

    print("Parameters used")
    print("B {}, C {}, D {}, N {}, e {}".format(rng.B, rng.C, rng.D, rng.N, rng.e))

    #print("{}: {}".format(0, rng.get_state() ))
    
    internal_state = [rng.rng_state]
    external_state = [rng.get_state()]

    print("Beginning countdown...")
    #Step RNG and save internal and external states
    for i in range(1,10):
        rng.step()
        internal_state.append(rng.rng_state)
        external_state.append(rng.get_state())

        #print("{},".format(rng.get_state() ))

    #print("internal_state = {}".format(internal_state))
    print("external_state = {}".format(external_state))

    with open("countdown", "w") as g:
        g.write("countdown = {}".format(external_state))

countdown:

countdown = [114192069133794974380732305590921198577882955526181826168062989591133080115022890196434131801813021076526261348606786043152436520971958947157510121292576547311043400809856921321547321991242323703524471848855041798207529472388014504596999593234820205756361893166928934862941526167848413119920879435418299587287, 50646327212718347056881627527537034547216799366473097665365776097250261006221084029628705467558651286312167712760377691033455593407975486158686678618096344722218342319763092547972813308450083933066369009248193497713782418749442015334394433178891642637515639152737768399876267026838198982774928685990852476258, 30639954235505686565884179906420547160100000919127996807433363914877591835785422695758054276969398807059285195052079919626729435767607222499537376617219911800727864846300771585300873516723473290552618663360400630892547636117775945566995389216243561055027630880550962971333700649588455115852874141298977961213, 32312136311887535797574953554646000671096404193652810990062981594205955148963671289375960729493319581952216253612878244657001410694864799034876978943539882827456573617313187886558272372942240260589141411040918098939502126844612576408868823415433155930035038531029602846817746195854154491411024807346862587573, 10568672705861325021195071081821257962441305083196243142085476319666340627892544463542185720644424300327100592431084292927624059278339403684417947863101558950579649138712139721305601459194246185922570850911599076172720061965389061057018641933852952791055213681855916905365180017467024827587157533452831045921, 93089895047622770408415775694863666367879486820316799478456884312093953332843967005074261370212843748558377091062898022061086734718391447161362831711810710122476560146883836025648297705926911230566796280989443289832915406930397275722898664838988611228405365299007729784213120090168549073092303329107009955779, 6748451440378230817719917277258448319301693263363819474626451620747822846876509377020197930162788292704374493286979984502648702599946766442234403275288918448091242495303751796482723355409491676244080729788229226355310318524997683994098847582280409270825645540597620590388505355656716578743244428756475490882, 57139241510576879909942116276068740343081355657009111034060235318309575135641513019213771795203029725415058452566199123924481022313304237777450702113942219653705144249790123639186375385197401982027444187153406284157811136421408064756192296883860380331785447007924739603174260080537995365696696823053931691356, 58867921609952411414595366694125588998402231337306940208872186061482465922501361534466146197293821511043183776063878036406896681193554941130488785264719536757196376927629643453214215661986778812473426240938053084216028097281222314747814336537385504098268815198657800230421073084066090655971243987892138600502, 49891161718446063251269564808167902260420455173432719160614170601286968077969094043131923740612029135195168823247725751770868318741904909821484591347622095775683165455423898746760930025196617165971733037089263446482936328059845507070571404802485217922894361546944330383019843908758663902211592246039234478733]

The flag is used as a seed to an RNG which combines a simple cubic congruential generator and a Blum Blum Shub RNG. We are given multiple outputs of the RNG.

Solution

The goal is to recover the seed. It is well known that the original seed of congruential generators can be easily recovered given enough outputs. However, we aren't given the output of the congruential generator. Instead, we are given the output squared, modulo $N$ . Computing the square root of a number modulo $N$ is equivalent to factoring $N$ , and in the challenge, $N$ is a product of two large primes which cannot be easily factored.

The trick to solving this problem is noticing that we have multiple polynomial equations in a single variable - the seed, because everything is dependent on the seed. Specifically, let $s$ be the seed (i.e. the flag as an integer), and let $c_1$ and $c_2$ be the first and second outputs of the RNG. Then, we have the following relations:

\begin{cases} s^e - c_1 \equiv 0 \pmod N \\ (Bs^3 + Cs + D)^e - c_2 \equiv 0 \pmod N \end{cases}

Now let $f_1(x) = x^e - c_1$ and $f_2(x) = (Bx^3 + Cx + D)^e - c_2$ . These polynomials both have $s$ as a root. Therefore, $(x - s)$ divides both polynomials. Computing the GCD of two polynomials with a maximum degree of $n$ can be done in quasilinear time in $n$ . In our case, $e = 2$ , so a simple Euclidean algorithm suffices to find the flag under a second.

from Crypto.Util.number import long_to_bytes

pgcd = lambda g1, g2: g1.monic() if not g2 else pgcd(g2, g1%g2)

B = int.from_bytes(b'BSides CBR', byteorder='big')
C = int.from_bytes(b'cybears', byteorder='big')
D = 2020
N = 133329403635104636891429937256104361307834148892567075810781974525019940196738419111061390432404940560467873684206839810286509876858329703550705859195697849826490388233366569881709667248117952214502616623921379296197606033756105490632562475495591221340492570618714533225999432158266347487875153737481576276481
e = 2
c1, c2 = [114192069133794974380732305590921198577882955526181826168062989591133080115022890196434131801813021076526261348606786043152436520971958947157510121292576547311043400809856921321547321991242323703524471848855041798207529472388014504596999593234820205756361893166928934862941526167848413119920879435418299587287, 50646327212718347056881627527537034547216799366473097665365776097250261006221084029628705467558651286312167712760377691033455593407975486158686678618096344722218342319763092547972813308450083933066369009248193497713782418749442015334394433178891642637515639152737768399876267026838198982774928685990852476258]

P.<x> = PolynomialRing(Zmod(N))
f1 = x^e - c1
f2 = (B*x^3 + C*x + D)^e - c2
m = -pgcd(f1, f2).constant_coefficient()
print(long_to_bytes(m))

Flag: cybears{B0mb_D1sp0sal_kitt3h_cutz_th3_r3d_w1r4}

Optimal Prime

We've managed to intercept some encrypted messages and some kind of binary related to them. Can you help?

We are given a binary and the file created by the binary. A sample output of the binary:

p_approx = 5209884374292238999298505347496882910653422994393667899822759690124744225285751900471624411052919181779471991930693046841341105505788271653260707111269219
q_approx = 5258167685109344334365155988744186539554842505818431072403969058394831881823343728221077864638246543574075336412011862666843749700206131830633205467018355
#GENERATING PRIME 1
#generatePrime(cybears):
p = 5209884374292238999298505347496882910653422994393667899822759690124744225285751900471624411052919181779472599172688757143688322040543798205146766335082231
#GENERATING PRIME 2
#generatePrime(dtss):
q = 5258167685109344334365155988744186539554842505818431072403969058394831881823343728221077864638246543574075171822769944500540526661664785901751965587836773
n = 0x2702cff2c7b384e9739b57b927512dc1b26b7f55139e8d175cf32157eca42b2320e3c8b8091c96ed2816cf1d01479465534ba1639076d238773f371618a5f3c38767d97baa98ca602bf343c58c36b5faa5b7883f0f7a146dc681288427749537ec236f1c9fb4a3afb007c3e69e742520e2acaa76bc51237a322d28f82e459073
#Encrypted message
plain1 = 15705819183902401214589605115852204071260905537696207244949389881577209929429511926414629809721660002601282328731880326389378653064233185913
cipher1 = 0x26cf94b586f65cded08f382b16933484632cdb0fa849bb02afe68c0cd5436b2cbb137111dbfc87e6d9076a68b0ddc903637b2a6aa02706d13c272f11a81ea1665f519baf350e2ff5004828a97a264ed98b3eb216aaafb1807f4296700911c877b8794b91aed7b15cee4730eca9224832d5939eab9cdf55f97408236c0a2ac063
plain2 = 117284182924575465559634442253159754088250862535188576927377502533101514343
cipher2 = 0x933c69fa38095ce39a5d01bf2924b7325963e18aadd0234826992defedd10c31a6fa6d0a3fc76da8e79eacf7b94365eede919ce4f725fc83641f0ea37ceb05a74690ccde7094de0ba089fb624c9f24dc58e5a02d20d19313dcb27abe3935e35aed2e4d489910cc10a88f355ba2fd594777030e2b5a710b9aac6416ce36e9316
plain3 = 179369493943865399967037721942028004410834463667216880684400465497503493949463823448688504833775644621525188184595588345714
cipher3 = 0x1048cc8a990ec333265929957293e14528dfb78db5565f1a3a5f0afc444554b323baf7847515ff0bb8b28b55a7bcef212614b279d0f9a7c6cb69661b3771a4566723b14676a06692a597c321e77d1d4e36b28ad8ce247ba2e70131fee19f31b1669f9a79f8d27e29b3c0825b62f79ea4a98c74a4b00771bf97e730578b88e955
i_flag = 7614254543332793982301013509499134750586024523680701204926582567827311681800425471101513660489442405124959794636230410494018889650285951342086664479628514235117381027262966749985917140382359692253331456
enc_flag = 0x136c9bbc7f88f2dad7892b48430318fa75ba21146701fef0d54f96475f5ade0b05d1613891ca71fe8b95be5f748b489db3c4e4ad3a2d9d8709187fe882c967d7fa1ec3393e10ee55a3c437780c17b5c0c4d91c2708cc8d523c0c2ae141acc6ea8414522cfa30a11e8f9c3f22246055a2e5b05f0f723f43950b041d4329e0653c

The output file contains cipher1, cipher2, cipher3 and enc_flag.

Solution

Without doing much reversing, we can see from the output that two prime numbers are generated and to form an RSA modulus, and three known messages are encrypted. The encrypted flag is also given. p_approx and q_approx are constant; they remain the same every time the program is run. There is a well known technique to recover RSA primes when partial knowledge of either prime is known. With the sample data, we see that p_approx approximates p accurately for all but the lower 160 bits.

Let $p'$ be the approximation for $p$ and consider the following univariate polynomial in $x$ :

f(x) = x + p'

Notice that $f(x)$ has a small root modulo $p$ (and that $p$ is a factor of $N$ ). We can use Coppersmith's theorem to solve for this small root. Once we have the root, we can recover $p$ and decrypt the ciphertext with textbook RSA.

One issue still remains: we aren't given $N$ . Fortunately, we are given three plaintext/ciphertext pairs, and this is enough to recover $N$ . Notice that $c_1 \equiv m_1^e \pmod N$ and $c_2 \equiv m_2^e \pmod N$ , so $\gcd(c_1 - m_1^e, c_2 - m_2^e)$ will be a multiple of $N$ . To get $N$ itself, we simply divide away the small multiples if there are any.

from Crypto.Util.number import long_to_bytes

e = 0x10001
p_approx = 5209884374292238999298505347496882910653422994393667899822759690124744225285751900471624411052919181779471991930693046841341105505788271653260707111269219
q_approx = 5258167685109344334365155988744186539554842505818431072403969058394831881823343728221077864638246543574075336412011862666843749700206131830633205467018355
m1 = 15705819183902401214589605115852204071260905537696207244949389881577209929429511926414629809721660002601282328731880326389378653064233185913
m2 = 117284182924575465559634442253159754088250862535188576927377502533101514343
c1 = 4639429435868417791580946287993466892654315993847175726850580087885491379369904007619141127820891005665779545413630538246230232695528160538607954814649727199405371120342472759319049912378744856724667125939378076464020073025347417498671824358873515185310946496281655504489713674691625088603497790738640141091
c2 = 10785692767471061167867917903131241160860940176448237621334399653692195000850598249500449968690440568757404157855906759946965019335481103246339629922146262178689029451817344459169313237639350951644787083257180599863643330385353301411115548468501778265590677255045583507693410873588388983761218779649939347598
c = 17102358272735099217312506685614452988708587713718155660998368165571542991606759345474827888210031715141101012679530733940952144484066071631561874453969210292583025259112261826247895219177382800836356087589130126656104288571004031140227980369245806926327700863559071209998424801836064908360376449835605471730

N = gcd(c1 - m1^e, c2 - m2^e)
for i in range(1, 10000):
    if N % i == 0:
        N //= i
P.<x> = PolynomialRing(Zmod(N), implementation='NTL')
f = x + p_approx
d_p = f.small_roots(X=2^160, beta=160/1024)[0]
p = p_approx + d_p
q = int(N)//int(p)
d = pow(e, -1, (p-1)*(q-1))
m = pow(c, d, N)
print(long_to_bytes(m))

Flag: cybears{Knock Knock, whos there? Lattice. Lattice who? Lattice in its cold outside!}

supergm

On a long journey to fetch the scriptures back to Cybeartron, the pilgrims pass through so many lands, all so different, that the most unlikely things become possible.

Perhaps these scriptures contain the keys to enlightenment?

We are given a file containing the parameters for a polynomial Goldwasser-Micali cryptosystem, as well as the encrypted flag.

Solution

Goldwasser-Micali is a cryptosystem whose security is based on the assumed hardness of determining whether an element in $\Z/N\Z$ is a quadratic residue, where $N$ is a product of two unknown large primes. Before encryption, a random element $x$ is chosen such that $x$ is a quadratic nonresidue modulo $N$ (note that this can be determined, since the party encrypting will know the factorisation of $N$ ). To encrypt a single bit $b$ , a random value $y$ is chosen and the ciphertext is computed as $c = y^2 x^b \pmod N$ . For decryption, notice that $c$ is a quadratic residue if and only if $b = 0$ , so if we find that $c$ is a quadratic residue, then we understand that $b = 0$ , and otherwise, $b = 1$ .

In the context of the challenge, instead of working over a ring of integers modulo $N$ , we work in the quotient ring $\mathbb{F}_3[x]/\langle N(x) \rangle$ . However, polynomials are much easier to factor than integers, so we can easily find two irreducible polynomials $p(x)$ and $q(x)$ such that $N(x) = p(x)q(x)$ . To decrypt the message, we need to check whether each ciphertext polynomial is a quadratic residue in $\mathbb{F}_3[x]/\langle N(x) \rangle$ . This can be done by checking if it is a quadratic residue in both $\mathbb{F}_3[x]/\langle p(x) \rangle$ and $\mathbb{F}_3[x]/\langle q(x) \rangle$ , which is handled easily with Sage's .is_square() method.

from Crypto.Util.number import *
P.<X> = PolynomialRing(GF(3))
load('./handout.sage')

p, q = factor(N)
Rp.<Y> = GF(3^255, modulus=p[0])
Rq.<Z> = GF(3^257, modulus=q[0])

flagbin = ''.join(str(1-int(Rp(c).is_square() and Rq(c).is_square())) for c in cipher)
print(long_to_bytes(int(flagbin, 2)).decode())

Flag: cybears{ROLYPOLYGMEZPZ}

Super Cool Facts Server!

It is the beginning of wisdom to say "I don't know."

Go forth and seek knowledge. This must be protected. We need to give them to you securely.

nc scf.chal.cybears.io 3141

SuperCoolFactsServer.py EC.py

We are given the source code for a service that provides us with encrypted super cool facts. We have the option to provide our own public point to be used in a ECDH key exchange to establish a shared secret key which is used to encrypt the facts. To get the flag, we have to guess what the server's private key is.

Solution

The fact that a homemade EC implementation is used is highly suspicious. Straight away, we see that we can provide our own point and the server will accept it without checking whether or not the point actually lies on the curve. This allows us to perform an invalid curve attack to recover the server's private key.

Recall that an elliptic curve over a field $\mathbb{F}_p$ can be described with the equation $y^2 \equiv x^3 + ax + b \pmod p$ . The addition formula for adding two points $(x_1, y_1)$ and $(x_2, y_2)$ is defined by

\begin{aligned} x_3 &\equiv \lambda^2 - x_1 - x_2 \pmod p \\ y_3 &\equiv \lambda (x_1 - x_3) - y_1 \pmod p \end{aligned}

where

\begin{aligned} \begin{cases} \lambda &= \frac{y_2 - y_1}{x_2 - x_1} &\qquad \text{if } x_1 \neq x_2 \\ \lambda &= \frac{3x_1^2 + a}{2y_1} &\qquad \text{if } x_1 = x_2 \end{cases} \end{aligned}

The key insight is that addition does not depend on $b$ at all, however, $b$ affects the order of the curve.

Suppose that we choose a $b$ such that the order, $q$ , of the curve $E_{a, b}(\mathbb{F}_p)$ has a small factor $m$ . Let $G$ be a generator of this curve. Then the point $G' = (q/m)G$ has order $m$ . If we send this point to the server as our public point, the server will compute $P = dG'$ (where $d$ is the server's private key) and use this point to compute the shared secret. Since the order of $G'$ is $m$ , then we can determine $k \equiv d \pmod m$ by bruteforcing $k \in [1, m)$ such that using $kG'$ as the shared secret point allows a successful decryption of a super cool fact.

Now, we repeat this process with different values of $b$ , and eventually we gather a lot of relations of the form $k_i \equiv d \pmod{m_i}$ . By the Chinese Remainder Theorem, if we have such relations where the $m_i$ are coprime and $\prod m_i > d$ , then we can solve for $d$ . This allows us to recover the private key.

import os
os.environ['PWNLIB_NOTERM'] = 'True'
from pwn import *
from json import loads, dumps
from tqdm import tqdm
import hashlib
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad

def kdf(shared_point):
    s = str(shared_point.xy()[0]) + str(shared_point.xy()[1])
    return hashlib.sha1(s.encode("utf-8")).digest()[0:16]

def decrypt_fact(ct, key, iv):
    cipher = AES.new(key, AES.MODE_CBC, iv)
    m = cipher.decrypt(ct)
    return m

def get_fact(pub_point):
    conn.sendlineafter('Enter a value: ', '1')
    conn.recvline()
    their_point = loads(conn.recvline().decode())
    conn.sendlineafter('Provide your public point:', dumps({ 'x': int(pub_point.xy()[0]), 'y': int(pub_point.xy()[1]) }))
    conn.sendlineafter('Enter a value: ', '2')
    ct = loads(conn.recvline().decode())
    return bytes.fromhex(ct['iv']), bytes.fromhex(ct['cipher'])

def solve_ord(G, order, fac):
    G_ = G * int(order / fac)
    iv, ct = get_fact(G_)
    for k in tqdm(range(1, fac)):
        key = kdf(k*G_)
        m = decrypt_fact(ct, key, iv)
        if b'COOL FACT' in m:
            print(unpad(m, 16).decode())
            return k

p = 273540544991637969479760315194669352313
q = 273540544991637969474690923574060066154
a = 27999486208995955
conn = remote('scf.chal.cybears.io', 3141)

K = []
M = []
while prod(M) < q:
    b = randint(1, 13333333337)
    E = EllipticCurve(GF(p), [a, b])
    G = E.gens()[0]
    order = E.order()
    facs = order.factor()
    if len(facs) < 5:
        continue
    f = order.factor()[4][0]
    if f.nbits() > 16 or f in M:
        continue
    k = solve_ord(G, order, f)
    if k:
        K.append(int(k))
        M.append(int(f))
secret = crt(K, M)

conn.sendlineafter('Enter a value: ', '3')
[conn.recvline() for _ in range(2)]
s = hashlib.sha1(str(secret).encode("utf-8")).hexdigest()
conn.sendline(s)
print(conn.recvline().decode())

Flag: cybears{TheVirginiaStateFlagIsTheOnlyUSStateFlagToFeatureNudity}

Ordinary Course of Business

We want so much when we need so little. But the illumined man wants for nothing.

The weary cybears travellers come across a strange bot. Every time they talk to it, it comes back with gibberish and nonsense. Could it be sprouting sage-like wisdom? Or be the ravings of a dysfunctional machine?

nc business.chal.cybears.io 3141

We are given a binary and a service to connect to. A teammate helped with the reversing and figured out there was a backdoor accessable via option 0 to unlock a secret menu using the password GreatSageEqualOfHeaven. Within the secret menu, we get access to an AES-OCB encryption and decryption oracle, and we can also obtain an encryption of the flag.

Solution

The goal is to recover the plaintext of a ciphertext using the encryption and decryption oracle. After a bit of Googling, we found this paper which describes an attack to recover the plaintext for any given ciphertext given access to an encryption and decryption oracle. Even better, we found a PoC online. All we had to do was adapt the oracle script to work with the server, and include the additional data "cybearsctf" in encryptions and decryptions where necessary.

oracle.py:

#!/usr/bin/env python3
from pwn import *
from block import Block

class Oracle:
    def __init__(self):
        self.r = remote('business.chal.cybears.io', 3141)
        self.r.recvuntil('q) quit\n')
        self.r.sendline('0')
        self.r.sendlineafter('password: ', 'GreatSageEqualOfHeaven')
        assert b'admin' in self.r.recvline()

    def get_chall(self):
        self.r.sendlineafter('q) quit\n', '3')
        self.r.recvline()
        C = bytes.fromhex(self.r.recvline().decode().strip().split('Cipher: ')[1])
        N = bytes.fromhex(self.r.recvline().decode().strip().split('Nonce: ')[1])
        T = bytes.fromhex(self.r.recvline().decode().strip().split('Tag: ')[1])
        return Block(C), Block(N), Block(T)

    def encrypt(self, N, M, tag=None):
        self.r.sendlineafter('q) quit\n', '1')
        self.r.sendlineafter('hex: \n', M.hex())
        self.r.sendlineafter('hex: \n', '-' if tag is None else tag.hex())
        self.r.sendlineafter('hex: \n', N.hex())
        C = bytes.fromhex(self.r.recvline().decode().strip().split('Cipher: ')[1])
        N = bytes.fromhex(self.r.recvline().decode().strip().split('Nonce: ')[1])
        T = bytes.fromhex(self.r.recvline().decode().strip().split('Tag: ')[1])
        return Block(C), Block(T)

    def decrypt(self, N, C, T, tag=None):
        self.r.sendlineafter('q) quit\n', '2')
        self.r.sendlineafter('hex: \n', C.hex())
        self.r.sendlineafter('hex: \n', '-' if tag is None else tag.hex())
        self.r.sendlineafter('hex: \n', N.hex())
        self.r.sendlineafter('hex: \n', T.hex())

        auth = b'Success' in self.r.recvline()
        if auth:
            M = bytes.fromhex(self.r.recvline().decode().strip().split('Message: ')[1])

        return auth, Block(M)

Flag: cybears{--=== T0t4lly_l3g1t1m4t3_bu51n355 ===--}

Rot Away Rust

Even in shadow, one may meet another, find a friend, and learn from him.

Connect to the server to see your friends and get a "guest" key!! You'll then be able to test your client by talking with the echo-bot (you'll need to establish a session key through the server first). Don't worry about the other users, they won't even talk to you unless you're their friend!

server - nc rar.chal.cybears.io 9000

clients - nc rar.chal.cybears.io [ports_provided_by_server]

using the provided client_initiator - python3 client_initiator.py -s rar.chal.cybears.io -p 9000 -t rar.chal.cybears.io -q [echo_bot_port]

client_initiator.py client_responder.py server.py rotawayrust.png rotawayrust.plantuml

This is a rather complex challenge. There are multiple services running; one of them is a "central" server which holds all of the clients keys and is used to establish a shared key between clients, and the others are clients that we can communicate with using the provided client_initiator.py file. We can use the guest account as the key is known, but can only talk to the echo server. To obtain the flag, we must talk to Flagimus Prime (the client running on port 9001), however, this client doesn't respond to us since we're just a mere guest!

Solution

To begin talking to Flagimus Prime, we need to pretend to be another client who Flagimus Prime is friends with. We'll pretend to be Ursine Magnus (client id 9003) who is affiliated with the cybears. Doing this, we'll be able to get in touch with Flagimus Prime, but the problem is that, because we don't know Ursine Magnus' key, we won't be able to request a shared key from the server as we won't be able to forge a valid AES-GCM ciphertext and tag.

It turns out that we can actually skip establishing a shared secret with the server all together as there is a vulnerability in the way the client responder parses the shared key. Specifically, in client_responder.py:107 (step2s):

(step2c, step2tag) = e2.encrypt_and_digest(nonce_b + session_id + id_a_packed + id_b_packed)

Flagimus Prime encrypts nonce_b || session_id || ID_A || ID_B with its key K_BS and sends it to us. Note that nonce_b is 4 bytes, session_id is 8 bytes, and ID_A and ID_B are 4 bytes each. Later on in the protocol (step5r), client A sends a payload encrypted with K_BS which is supposed to contain nonce_b || K_AB to establish the shared key (note that client A is supposed to receive this ciphertext from the server and forwards it to client B).

However, when Flagimus Prime receives this ciphertext and tag, it decrypts and verifies it, and then sets the shared key to the last 16 bytes of the plaintext (client_responder.py:168):

step5_dec_nonce, step5_dec_k_ab = struct.unpack('4s16s', step5_plain)

Since Flagimus Prime gives us a valid ciphertext/tag of nonce_b || session_id || ID_A || ID_B in step 2, we can simply forward this to it in step 5 and it will take session_id || ID_A || ID_B as the shared key, but this contains data that we know! When we receive Flagimus Prime's encrypted message, we'll be able to decrypt it.

from pwn import *
from Crypto.Cipher import AES
import json

conn = remote('rar.chal.cybears.io', 9001)
conn.sendline(json.dumps({ 'ID_A': 9003 }))
step_2r = json.loads(conn.recvline().decode())
conn.sendline(json.dumps(step_2r))
step_5r = json.loads(conn.recvline().decode())

key = bytes.fromhex(step_2r['session_id']) + int(9003).to_bytes(4, 'little') + int(9001).to_bytes(4, 'little')
ct = bytes.fromhex(step_5r['gcm_cipher'])
nonce = bytes.fromhex(step_5r['gcm_nonce'])

cipher = AES.new(key, AES.MODE_GCM, nonce)
msg = cipher.decrypt(ct)
print(msg.decode())

Flag: cybears{Typ3s_0f_C0nfu510n}